Chapter 6 ランダム化比較試験
6.1 ランダム化比較試験の解析
ランダム化比較試験 (randomized controlled trial, RCT) とは、評価のバイアス(偏り)を避け、客観的に治療効果を評価することを目的とした研究試験の方法です。 研究対象者を2群以上に分けて、介入開始前と介入開始後で治療効果があったかどうかを評価します。 RCTにおいてランダム化は必須で、これによって群間のバイアスがなくなると考えられています。
ランダム化比較試験は、2群 (group, arm) 以上の群が、2回以上評価を受けます。
| arm | pre | post |
|---|---|---|
| A | mean\(_{Apre}\) | mean\(_{Apost}\) |
| B | mean\(_{Bpre}\) | mean\(_{Bpost}\) |
表のように、4つ以上のの平均値を比較する必要があります。 では、どのようにしたら、比較ができるでしょうか?
以下のような考え方が思いつくと思います。
- mean\(_{Apre}\) と mean\(_{Apost}\) に有意差があり、mean\(_{Bpre}\) に mean\(_{Bpost}\) 有意差がなければ、A は有意に変わった。
- mean\(_{Apost}\) - mean\(_{Apre}\) と mean\(_{Bpost}\) - mean\(_{Bpre}\) に差があるかどうかを検定する(差の差検定)。
- mean\(_{Apre}\) と mean\(_{Bpre}\) には差がないはずだから、 mean\(_{Apost}\) と mean\(_{Bpost}\) だけ検定すればよい。
上記のような手法が使われることもありますが、実際には以下のように行われています。
- 時間と群に交互作用があるかどうかを検定する。
この交互作用を検定する手法が、分散分析 (Analysis of Vaiance, ANOVA) です。 RCTにおける分散分析においては、同じ被験者を繰り返し評価するため、これをとくに「繰り返しのある分散分析 (repeated measure ANOVA」といいます。 繰り返しのある分散分析では、対応のある検定を行うため、対応のない検定とは異なる計算方法を用います。
6.2 論文 Holthoff VA (2015) PLoS One
ランダム化比較試験について、実際のデータを用いて解析を行ってみます。参考にする論文は、以下のものです。
Holthoff VA, Marschner K, Scharf M, Steding J, Meyer S, Koch R, & Donix M (2015) Effects of physical activity training in patients with Alzheimer’s dementia: Reslts of a pilot RCT study. PLoS One, 10(4), e0121478. https://dx.doi.org/10.1371%2Fjournal.pone.0121478
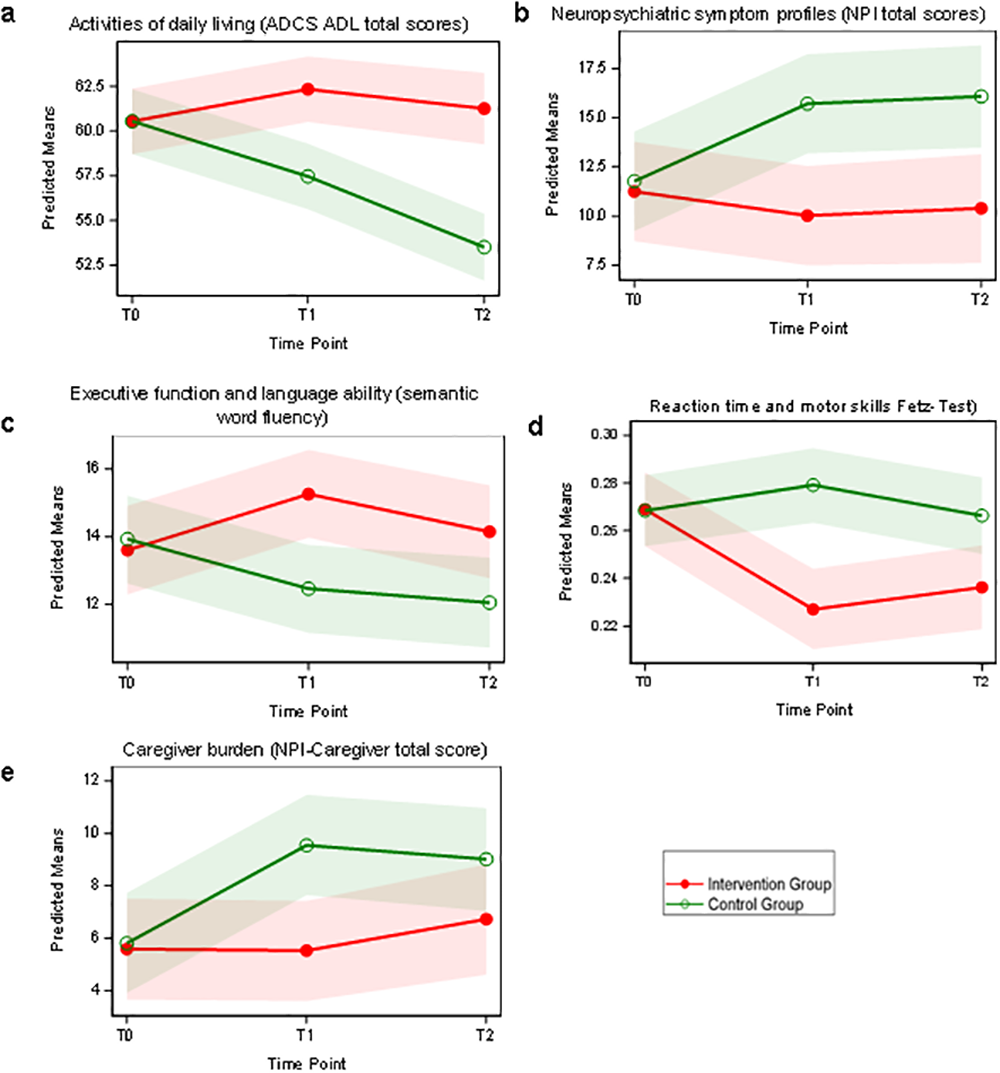
Figure 6.1: Holthoff (2015) Fig 2. a-e. Effects of physical activity on clinical performance.
6.3 SPSS データの読み込み
library(haven)
df3 <- read_sav("https://doi.org/10.1371/journal.pone.0121478.s003")
df4 <- read_sav("https://doi.org/10.1371/journal.pone.0121478.s004")6.4 表1の作成
では s004 から Table 1 を再現してみましょう。
library(tableone)
df4$BMI <- df4$Gewicht_kg / ( df4$Größe_cm/100 ) ^2
CreateTableOne(data = df4,
strata="group",
vars=c("Alter_in_Jahren_Studienbeginn","Geschlecht", "Ausbildungsjahre", "BMI"),
factorVars=c("Geschlecht"))## Stratified by group
## 1 2 p
## n 15 15
## Alter_in_Jahren_Studienbeginn (mean (SD)) 72.40 (4.34) 70.67 (5.41) 0.341
## Geschlecht = 1 (%) 8 (53.3) 7 (46.7) 1.000
## Ausbildungsjahre (mean (SD)) 12.33 (2.13) 14.13 (2.70) 0.052
## BMI (mean (SD)) 23.43 (2.75) 24.12 (4.06) 0.589
## Stratified by group
## test
## n
## Alter_in_Jahren_Studienbeginn (mean (SD))
## Geschlecht = 1 (%)
## Ausbildungsjahre (mean (SD))
## BMI (mean (SD))Number of steps のデータは見つかりませんでした。その他の値について、平均値と標準偏差は一致しました。 ただし、p値については多少異なっています。
df3 は、基本的には Long 形式ですが、横にも長いので、関心のある列のみ表示します。
datatable(df3[c("Patientennummer", "Gruppe", "Messzeitpunkt_Nummer", "ADCS_ges", "NPI_ges")])6.5 ADL(ADCS)の評価
まず、df3 が巨大なデータフレームなので、ADCSとその他必要なデータだけの小さなデータフレームを作成します。
最初に、行数をそろえるために、インデックス列をコピーします。最初に使う列をすべて指定してもよいのですが、ここではインデックス列のみとしました。なお、最初にすべてコピーする場合は、
df3ADCS <- df3[c("Patientennummer", "Gruppe", "Messzeitpunkt_Nummer", "ADCS_ges")]とします。列数が一つの時は文字列“A”ですが、複数の場合は文字列リストc(“A”, “B”, “C”) になります。
Time (Messzeitpunkt_Nummer) は、因子型にもとれますが、geom_smooth() を使うためには x軸も数値型である必要があるので、数値型とします。
library(ggplot2)
df3ADCS <- df3["Patientennummer"]
df3ADCS$Group <- factor(df3$Gruppe, level=c(1,2))
df3ADCS$Time <- as.numeric(df3$Messzeitpunkt_Nummer)
df3ADCS$ADCS <- as.numeric(df3$ADCS_ges)6.6 図の作成
6.6.1 ggplot
平均値と標準誤差を手動で計算する方法です。
library(dplyr)##
## 次のパッケージを付け加えます: 'dplyr'## 以下のオブジェクトは 'package:car' からマスクされています:
##
## recode## 以下のオブジェクトは 'package:MASS' からマスクされています:
##
## select## 以下のオブジェクトは 'package:imputeMissings' からマスクされています:
##
## compute## 以下のオブジェクトは 'package:stats' からマスクされています:
##
## filter, lag## 以下のオブジェクトは 'package:base' からマスクされています:
##
## intersect, setdiff, setequal, uniondf3Plot <- summarise(group_by(df3ADCS, Group, Time),
ADCS_means = mean(ADCS, na.rm=T),
ADCS_SEs = sd(ADCS, na.rm=T)/sqrt(length(ADCS)))## `summarise()` has grouped output by 'Group'. You can override using the `.groups` argument.ggplot(data = df3Plot, aes(x = Time, y = ADCS_means, group = Group, colour = Group)) +
geom_point(position = position_dodge(width=0.2)) +
geom_line(position = position_dodge(width=0.2)) +
geom_errorbar(aes(ymin=ADCS_means-ADCS_SEs, ymax=ADCS_means+ADCS_SEs),
width=.1, position = position_dodge(width=0.2))+
theme_bw()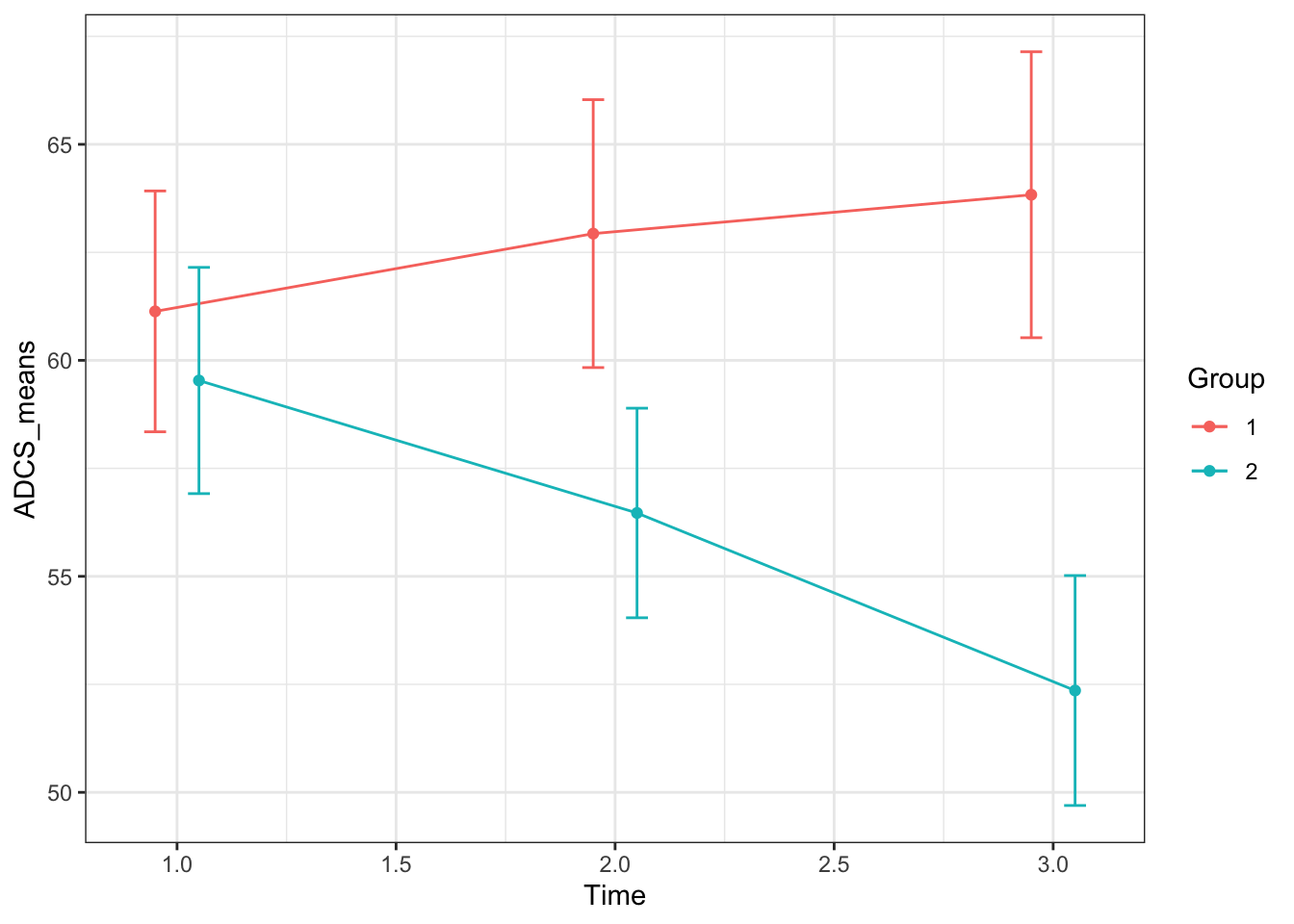
平均値と標準誤差を自動的にプロットする方法です。
6.6.2 ggpubr
library(ggpubr)
ggline(df3ADCS, x = "Time", y = "ADCS", add = "mean_se", color = "Group") +
stat_compare_means(aes(group = Group), label = "p.signif")## Warning: Removed 4 rows containing non-finite values (stat_summary).## Warning: Removed 4 rows containing non-finite values (stat_compare_means).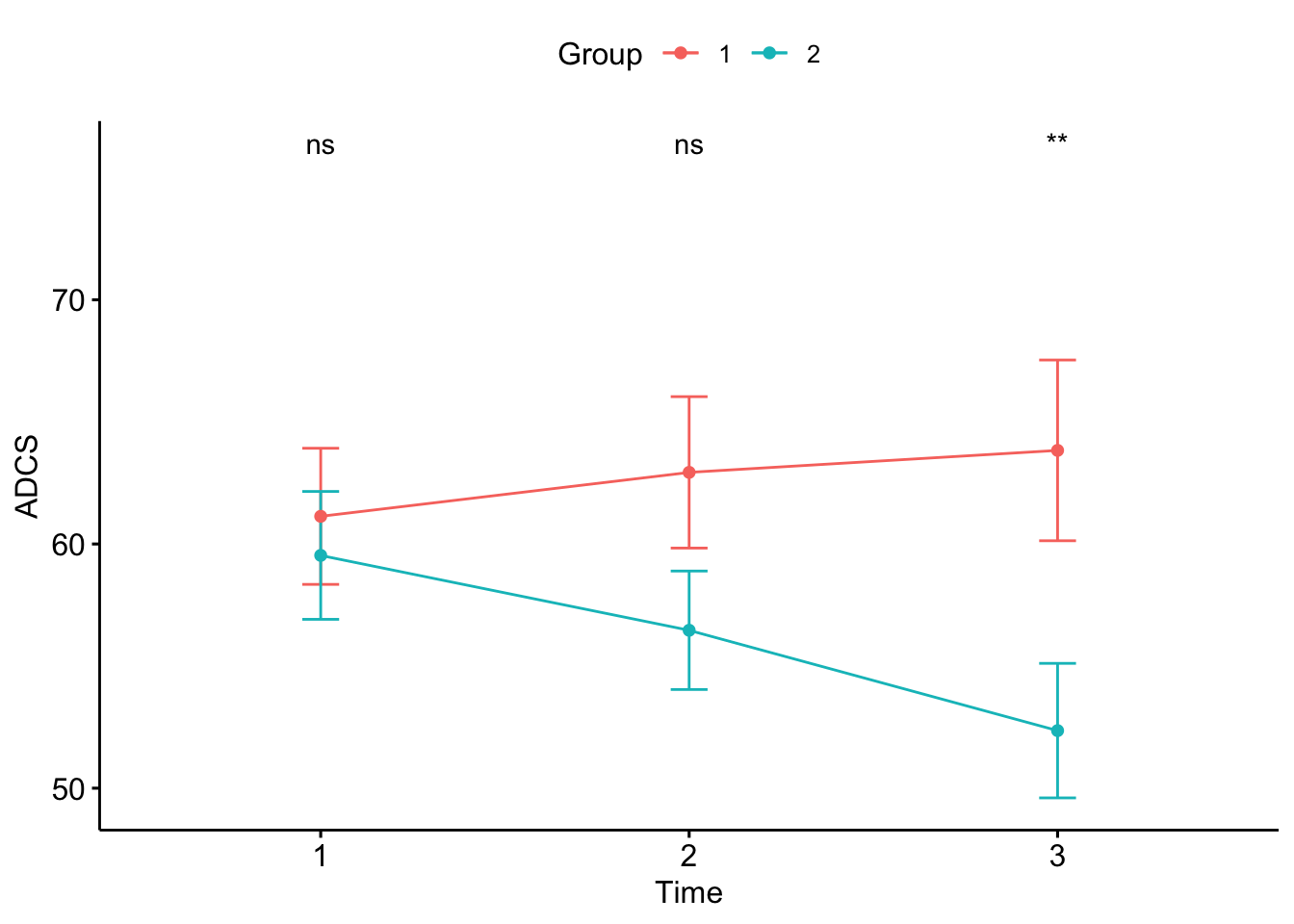
ggplot(data = df3ADCS, aes(x = Time, y = ADCS, colour = Group)) +
geom_smooth(method="lm")## `geom_smooth()` using formula 'y ~ x'## Warning: Removed 4 rows containing non-finite values (stat_smooth).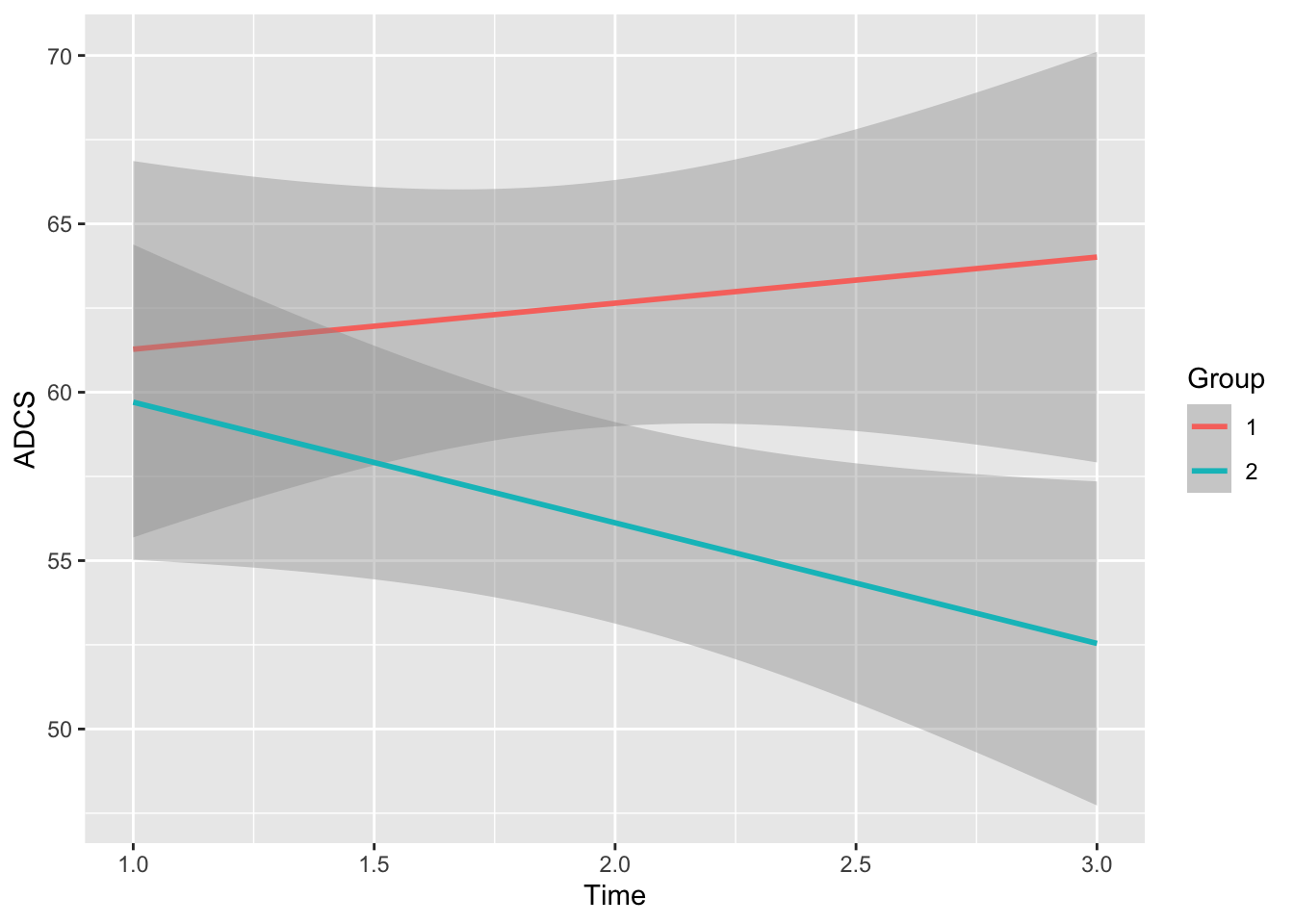
6.7 検定
6.7.1 two way repeated measures ANOVA
データのない行を削除し、 外れ値を確認します。
library(rstatix)
df3ADCSnoNA <- na.omit(df3ADCS)
identify_outliers(group_by(df3ADCSnoNA, "Group", "Time"), "ADCS")## [1] "Group" "Time" Patientennummer Group
## [5] Time ADCS is.outlier is.extreme
## <0 行> (または長さ 0 の row.names)df3ADCSnoNA <- na.omit(df3ADCS)
shapiro_test(group_by(df3ADCSnoNA, "Group", "Time"), "ADCS")残念ながら、これは以下のエラーが出ます。
Error: Problem with mutate() column data. i data = map(.data$data, .f, ...). x Can’t subset columns that don’t exist. x Column "ADCS" doesn’t exist. Run rlang::last_error() to see where the error occurred.
library(rstatix)
aovDf3ADCS <- anova_test(
data = df3ADCSnoNA,
dv = "ADCS",
wid = "Patientennummer",
within = c("Group","Time"))
get_anova_table(aovDf3ADCS)残念ながら、これは以下のエラーが出ます。
Error in lm.fit(x, y, offset = offset, singular.ok = singular.ok, …) : 0 (non-NA) cases
repeated measures ANOVA は、計測されていないデータがあると実行することができません。 例えば、Patientennummber = 11 の T3 におけるデータがありません(他にも何か所か欠測があります)。 このため、Patientennumber = 11 全体を削除するか、代入 (imputation) を必要があります。
介入後のフォローアップを伴う解析を予定している場合は、特に欠測が発生しやすいので注意が必要です。
削除するか、代入するかは、研究計画段階で決める必要があります。
6.7.2 Mixed model
一方、欠測値があっても実行できるのが Mixed Model の強みです。
library(lme4)
lmeModeldf3ADCS = lmer(ADCS ~ Group*Time + (1|Patientennummer), data=df3ADCS)
anova(lmeModeldf3ADCS)## Analysis of Variance Table
## npar Sum Sq Mean Sq F value
## Group 1 17.913 17.913 2.1771
## Time 1 144.112 144.112 17.5154
## Group:Time 1 213.016 213.016 25.8900library(jstable)
#tab_model(lmeModeldf3NPI)
lmer.display(lmeModeldf3ADCS)## $table
## coeff(95%CI) P value
## Random effects <NA> NA
## Patientennummer 109.44 NA
## Residual 8.23 NA
## Metrics <NA> NA
## No. of groups (Patientennummer) 30 NA
## No. of observations 86 NA
## Log-likelihood -261.03 NA
## AIC value 522.06 NA
##
## $caption
## [1] "Linear mixed model fit by REML : ADCS ~ Group * Time + (1 | Patientennummer)"library(emmeans)
emmeans(lmeModeldf3ADCS, list(pairwise ~ Group), adjust = "tukey")## $`emmeans of Group`
## Group emmean SE df lower.CL upper.CL
## 1 62.0 2.74 28.1 56.4 67.6
## 2 56.3 2.74 27.9 50.7 61.9
##
## Degrees-of-freedom method: kenward-roger
## Confidence level used: 0.95
##
## $`pairwise differences of Group`
## 1 estimate SE df t.ratio p.value
## 1 - 2 5.69 3.87 28 1.469 0.1529
##
## Degrees-of-freedom method: kenward-rogerここでは、 p = 0.1529 より、交互作用があったとは言えないと解釈します。
6.8 BPSD(NPI)の評価
library(ggplot2)
df3NPI <- df3["Patientennummer"]
df3NPI$Group <- factor(df3$Gruppe, level=c(1,2))
df3NPI$Time <- as.numeric(df3$Messzeitpunkt_Nummer)
df3NPI$NPI <- as.numeric(df3$NPI_ges)
#df3NPI <- subset(df3, !is.na(df3$NPI))
ggplot(data = df3NPI, aes(x = Time, y = NPI, colour = Group)) +
geom_point() +
geom_smooth(method = "lm")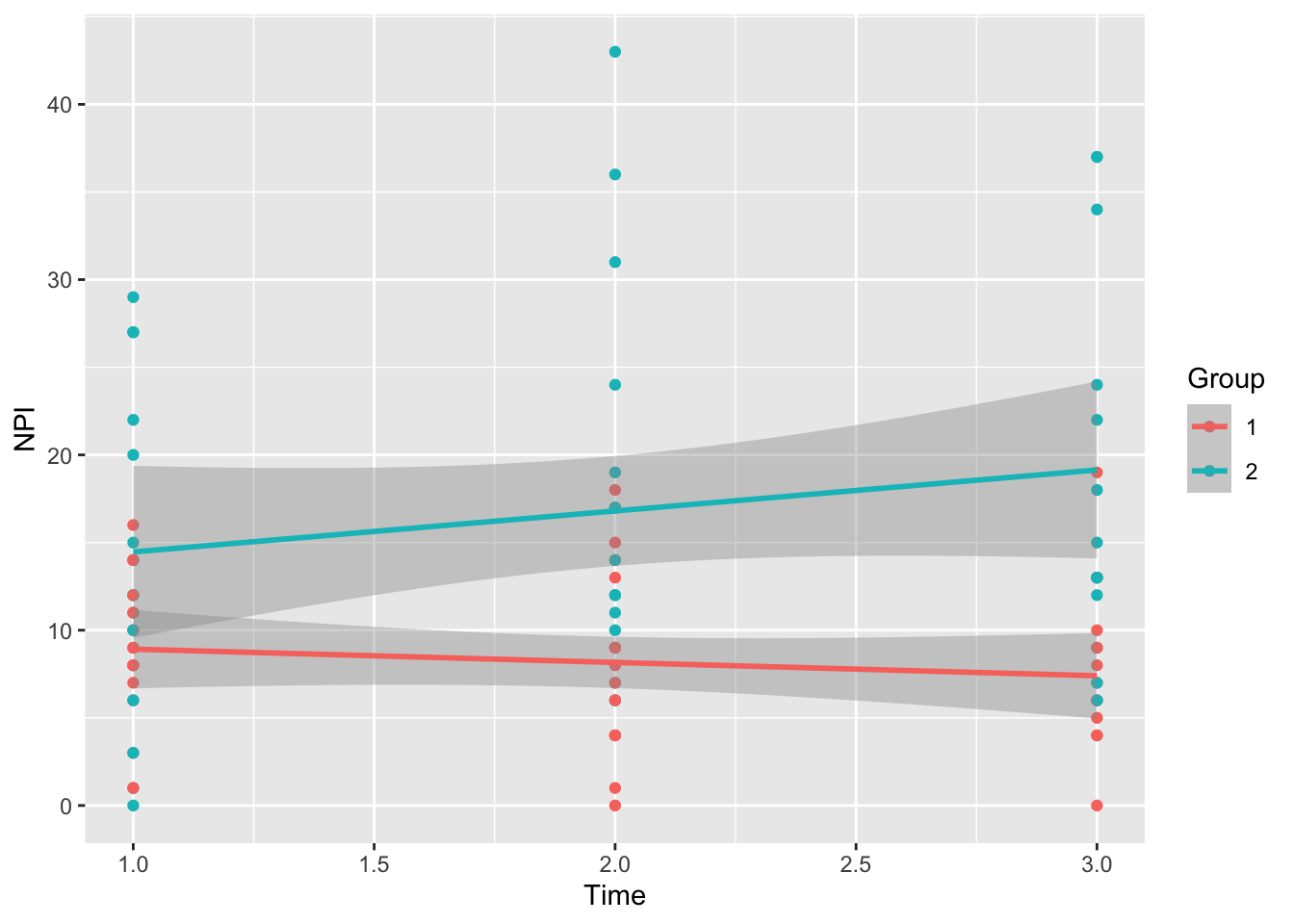
library(lme4)
lmeModeldf3NPI = lmer(NPI ~ Group*Time + (1|Patientennummer), data=df3NPI)
anova(lmeModeldf3NPI)## Analysis of Variance Table
## npar Sum Sq Mean Sq F value
## Group 1 139.782 139.782 9.2877
## Time 1 46.375 46.375 3.0813
## Group:Time 1 97.638 97.638 6.4875library(jstable)
#tab_model(lmeModeldf3NPI)
lmer.display(lmeModeldf3NPI)## $table
## coeff(95%CI) P value
## Random effects <NA> NA
## Patientennummer 49.65 NA
## Residual 15.05 NA
## Metrics <NA> NA
## No. of groups (Patientennummer) 30 NA
## No. of observations 86 NA
## Log-likelihood -267.34 NA
## AIC value 534.67 NA
##
## $caption
## [1] "Linear mixed model fit by REML : NPI ~ Group * Time + (1 | Patientennummer)"library(emmeans)
emmeans(lmeModeldf3NPI, list(pairwise ~ Group), adjust = "tukey")## $`emmeans of Group`
## Group emmean SE df lower.CL upper.CL
## 1 8.36 1.92 28.2 4.43 12.3
## 2 16.61 1.91 27.8 12.69 20.5
##
## Degrees-of-freedom method: kenward-roger
## Confidence level used: 0.95
##
## $`pairwise differences of Group`
## 1 estimate SE df t.ratio p.value
## 1 - 2 -8.24 2.71 28 -3.044 0.0050
##
## Degrees-of-freedom method: kenward-rogerp = 0.0050 なので、交互作用があったと解釈します。
6.9 サンプルサイズ
two-way repeated measues ANOVA
library(WebPower)
wp.rmanova(ng = 2,
nm = 3,
power = 0.80,
alpha = 0.05,
f = 0.32,
type = "2")## Repeated-measures ANOVA analysis
##
## n f ng nm nscor alpha power
## 95.61069 0.32 2 3 1 0.05 0.8
##
## NOTE: Power analysis for interaction-effect test
## URL: http://psychstat.org/rmanova6.10 ランダム化
RCT研究においては、ランダム化が必須です。 ランダム化とは、研究対象者に対して2群に分ける手法で、ランダム化を行うことにより、2郡に偏りがなくなると考えられています。
- 単純法: 無作為化の手法の中で最も単純な方法で、A群とB群にすべての患者を同じ確率で割り付ける方法
- 置換ブロック法: 最初にブロックのサイズを定義し、試験に参加する患者さんを順にブロックに入れていき、そのブロックの中でAとBそれぞれに割り付けられる研究対象者 6 の数を揃える方法。単純法で比較群間の研究対象者数が揃いにくいという欠点を補う
- 層別法: 比較群間で差が絶対に出てほしくない背景因子については「層別 」を行うことによって無作為化を行う
- 最小化法 (動的割り付け法): 研究対象者が入るたびに、ある特定の背景因子の比較群間の不均衡の程度をチェックし、 次に割り付けられる研究対象者の背景を考慮して、その不均衡を小さくする方向に割り付けを行う方法
まずは、単純法 (complete randamization) でランラム化列を作成します。 2群(A群, B群)として、被験者を、順にどちらの群に割り当てるかを示す割付列を表示します。
library(randomizeR)## 要求されたパッケージ plotrix をロード中ですparamRandomize <- crPar(10)
seqRandomize <- genSeq(paramRandomize)
seqRandomize##
## Object of class "rCrSeq"
##
## design = CR
## seed = 1235143119
## N = 10
## groups = A B
##
## The sequence M:
##
## 1 B A A B A A B A A Bこの方法は、現在は適切な方法とは考えられていません。 また、この方法ですと、サンプルサイズが小さいと、片方の群に偏ることもあります。
次に、ブロックサイズ4で置換ブロック法を行います。
paramRandomize <- rpbrPar(10, 4)
seqRandomize <- genSeq(paramRandomize)
seqRandomize##
## Object of class "rRpbrSeq"
##
## design = RPBR(4)
## rb = 4
## filledBlock = FALSE
## seed = 1199705343
## N = 10
## K = 2
## ratio = 1 1
## groups = A B
##
## RandomizationSeqs BlockConst
## A B B A B B A A ... 4 4 44人1組で必ずAとBが2回ずつ出現しています。
最小化法は、randomizeR ライブラリには複数の関数が用意されています。
一例として、Big Stick デザインで、最大不均衡を4とします。
paramRandomize <- bsdPar(10, 4)
seqRandomize <- genSeq(paramRandomize)
seqRandomize##
## Object of class "rBsdSeq"
##
## design = BSD(4)
## seed = 206479777
## N = 10
## groups = A B
## mti = 4
##
## The sequence M:
##
## 1 A B A A B B A B A Bこれで、群間の参加者の差が4以下になります。